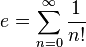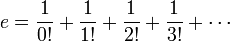numeros irracionales

En matemáticas, un número irracional es un número que no puede ser expresado como una fracción , donde  y  son enteros y  es diferente de cero. Es cual quier numero real que no es racional
¿Qué son números irracionales? Los números irracionales tienen como definición que son números que poseen infinitas cifras decimales no periódicas, que por lo tanto no pueden ser expresados como fracciones.

Para distinguir los números irracionales de los racionales, debemos tomar en cuenta que los números racionales si se pueden escribir de manera fraccionada o racional, por ejemplo: 18/5 que es igual a 3,6 por lo tanto es un número racional a diferencia de la raíz cuadrada de dos en cuyo resultado se obtienen infinito número de cifras decimales, y su fraccionamiento resulta imposible.

Podrías intentar encontrar la respuesta en una calculadora, y según el número de decimales con la cual la tengas programada, obtendrás algunos resultados: 1.4142135 esta es la respuesta de √2 con siete decimales, pero la cifra se irá alargando pues tiene infinitos decimales. De esta manera podemos definir a los números irracionales como un decimal infinito no periódico, es decir que cualquier representación de un número irracional, solo es una aproximación en números racionales.

Ejemplos de números irracionales

En primer lugar vamos a anotar los ya mencionados números irracionales algebraicos con ejemplos, ya habíamos hablado de √2 o raíz cuadrada de dos que resulta de una ecuación algebraica, pero también tenemos otros ejemplos que podrían resultar son:

1+3√2

y

 1+√3−−−−−−√4

Por otro lado, tenemos a los números irracionales trascendentes, que no pueden representarse mediante radicales como se lo ha hecho en el ejemplo anterior, sino que deben ser representados con decimales infinitos no periódicos, y con tres puntos suspensivos para denotar que son infinitos, de lo contrario estaríamos escribiendo números durante toda la eternidad, así:

0,1961325454898161376813268743781937693498749…

0,01001000100001000001000000100000001000000001…

numero pi

π (pi) es la relación entre la longitud de una circunferencia y su diámetro, en geometría euclidiana. Es un número irracional y una de las constantes matemáticas más importantes. Se emplea frecuentemente en matemáticas, física e ingeniería. El valor numérico de π, truncado a sus primeras cifras, es el siguiente:

Se le conoce también con el nombre de Constante de Arquímedes, quien lo calculó con la aproximación de  < π < , tal como consignó en su obra "Medición del círculo", ciertamente con otra notación.

numero e

La constante matemática 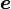 es uno de los más importantes números reales irracionales y trascendentes.¹ Se relaciona con muchos interesantes resultados. Por ejemplo, la derivada de la función exponencial  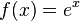es esa misma función. El logaritmo en base  se llama logaritmo natural o neperiano.

El número , conocido a veces como número de Euler o constante de Napier, fue reconocido y utilizado por primera vez por el matemático escocés John Napier, quien introdujo el concepto de logaritmo en el cálculo matemático.

Juega un rol importante en el cálculo y en el análisis matemático, en la definición de la función m

La definición más común de e es como el valor límite de la serie

que se expande como

Otra definición habitual⁶ dada a través del cálculo integral es como solución de la ecuación:

que implica

es decir que se define e como el número para el que

o lo que es lo mismo, el número para el que

suma de fracciones

Suma de fracciones con el mismo denominador:

Para sumar fracciones con el mismo denominador se tienen que suman los numeradores dejando el mismo denominador.

Por ejemplo,

Como las 2 fracciones tienen el mismo denominador, lo que tenemos que hacer es dejar el mismo denominador, que es 4, y sumar los numeradores:

3 + 2 = 5

Y el resultado de la suma de fracciones es

Suma de fracciones con distinto denominador:

Para hacer suma de fracciones con distinto denominador, lo primero que hay que hacer esponer un denominador común: esto es el mínimo común múltiplo entre los denominadores que haya. Después multiplicamos cada denominador por el número que hayamos multiplicado al denominador. Por último, sumamos los numeradores que hayamos obtenido y dejamos el mismo denominador.

Por ejemplo,

Lo primero es haya un denominador común entre el 3 y el 5. Para eso, hayamos el mínimo común múltiplo entre ambos.

m.c.m. (3,5) = 15

Por lo tanto 15 es el denominador común de las dos fracciones.

Ahora tenemos que multiplicar cada denominador por el número que hayamos multiplicado el denominador. Para ello, dividimos el m.c.m entre el denominador inicial y el resultado lo multiplicamos por el numerador de esa fracción:

Para la primera fracción:

15 : 3 = 5

5 x 2 = 10

Por lo tanto, 10 es el denominador de la primera fracción.

Para la segunda fracción:

15 : 5 = 3

3 x 4 =12

Por lo tanto, 12 es el denominador de la segunda fracción.

Ahora ya solo nos queda sumas los numeradores:

10 + 12 = 22

Y el resultado de la suma de fracciones es:

los numeros reales

Definición

Número real, cualquier número racional o irracional. Los números reales pueden expresarse en forma decimal mediante un número entero, un decimal exacto, un decimal periódico o un decimal con infinitas cifras no periódicas. El conjunto de los números realesNúmero Naturales (N): números con los que contamos (también se les llama enteros positivos. )
Enteros (E): conjunto de todos los números naturales con sus opuestos (negativos) y el cero. .
Racionales: conjunto formado por todos los números que se pueden escribir en la forma , donde m y n son enteros .
Número Reales (R): todos los racionales y los irracionales. Los números racionales tienen representaciones decimales repetitivas (periódicas), en tanto que los irracionales tienen representaciones no repetitivas infinitas.
 1.5.2 Representación geométricaSe pueden representar sobre una recta del siguiente modo: a uno de los puntos de la recta se le asocia el cero, 0. Se toma hacia la derecha otro punto al que se asocia el 1. La distancia del 0 al 1 se denomina segmento unidad y con ella se representan todos los números enteros.      Los restantes números reales (racionales o irracionales) se sitúan sobre la recta, bien valiéndose de construcciones geométricas exactas, bien mediante aproximaciones decimales. Es importante el hecho de que a cada punto de la recta le corresponde un número real y que cada número real tiene su lugar en la recta (correspondencia biunívoca). Por eso a la recta graduada de tal manera se la denomina recta real. 1.5.3 Definición de igualdad y sus propiedadesEl signo de igualdad (=) se emplea para unir dos expresiones, cuando ambas son los nombres o descripciones del mismo objeto.  significa que a y b son dos nombres del mismo objeto. Naturalmente , significa a no es igual a b.
 Si dos expresiones algebraicas con una o más variables se unen mediante el signo igual, la forma así obtenida recibe el nombre de ecuación algebraica. Propiedades de la igualdadSi a, b y c son nombres de objetos, tenemos:Propiedad reflexiva: Propiedad simétrica: Si , entonces: Propiedad transitiva: Si  y , entonces: Principio de sustitución: Si , cualquiera de las dos puede reemplazar a la otra en una proposición, sin alterar la verdad o falsedad de dicha proposición.

x

congruencias

sea N >1
se dice que dos enteros a  b su congruencia modulo m, si m/ a-b
a=b (mod m) <------> m/a-b
p/ej:
1 dos numeros pares a b son consiente modulo 2 y a que su diferencia a-b es divisible entre 2 es decir 10= 8(mod2) 2/10-8
=2/"
dos numeros impares (a d son tambien congruentes modulo 2 es decir:
21 a 15
21= 15(mod2) 2/21-15