PROGRAMA DE ÁLGEBRA SUPERIOR 2 SEGUNDO SEMESTRE
1.
EL ANILLO DE
LOS NÚMEROS ENTEROS.
1.1
Propiedades básicas de las operaciones en Z.
1.2
Propiedades de anillo de los enteros.
1.3
Dominios enteros.
1.4
El orden en Z.
1.5
Unidades.
1.6
Inducción.
2.
DIVISIBILIDAD.
2.1
Definiciones.
2.2
Propiedades elementales de la divisibilidad.
2.3
El algoritmo de la división.
2.4
El máximo común divisor.
2.5
Soluciones enteras.
2.6
El algoritmo de Euclides.
2.7
Factorización única.
2.8
Congruencias.
3.
EL CAMPO DE
LOS NÚMEROS REALES.
3.1
Los números racionales.
3.2
Definiciones.
3.3
Estructura de campo ordenado.
3.4
Los enteros como racionales.
3.5
Los números reales.
3.6
El orden en R.
3.7
Cotas y fronteras.
3.8
Operaciones con reales.
3.9
Propiedades de las operaciones.
3.10Estructura de campo
ordenado.
3.11Decimales periódicos
y racionales.
3.12Raíces de reales
positivos.
3.13Exponentes
racionales.
3.14Valor absoluto.
3.15Aproximación.
4.
POLINOMIOS Y
ECUACIONES.
4.1
Definiciones.
4.2
Los Polinomios como funciones.
4.3
Operaciones.
4.4
El algoritmo de la división.
4.5
Raíces de polinomios.
4.6
Ecuaciones de segundo grado.
4.7
División sintética.
4.8
Cálculo aproximado de raíces.
4.9
Factorización de polinomios.
4.10Raíces Múltiples.
4.11Derivadas y
multiplicidad.
4.12Coeficientes y
raíces.
4.13Polinomios con
Coeficientes reales.
4.14El algoritmo de
Euclides.
4.15Teorema de Sturm.
4.16Fracciones
racionales.
4.17Descomposición de
fracciones parciales.
4.18Ecuaciones de tercer
y cuarto grado.
 : números enteros significa ^=y
: números enteros significa ^=y E(-∞.+∞)
E(-∞.+∞) ¨{--------4,-3,.2,-1,0,1,,2,3,4,-----}
¨{--------4,-3,.2,-1,0,1,,2,3,4,-----} (básicas en las operaciones)
(básicas en las operaciones)
 →a+b=b+a
→a+b=b+a
 →(a+b)+c=a+(b+c)
→(a+b)+c=a+(b+c)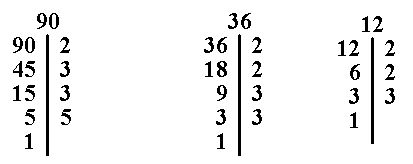
 entonces
entonces 
 es un entero,
es un entero, 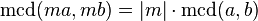
 es un número primo, entonces
es un número primo, entonces  o bien
o bien 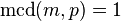
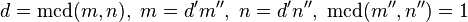 , entonces
, entonces 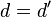
 es un divisor común de
es un divisor común de  , entonces
, entonces 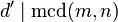
 , entonces
, entonces 
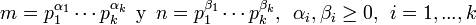 , entonces:
, entonces:
 5 + 6 + 4 = 15
5 + 6 + 4 = 15 
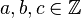 , es decir
, es decir  ,
,  y
y  son
son  (Propiedad Reflexiva).
(Propiedad Reflexiva). y
y  , entonces
, entonces  (Propiedad Transitiva).
(Propiedad Transitiva).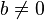 , entonces
, entonces 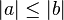 .
.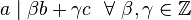 .
. , entonces
, entonces  .
. , entonces
, entonces  .
. ,
, 
 y
y 
 .
. y
y  para todo
para todo 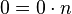 y
y  .
.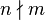 . Notemos que
. Notemos que  para todo
para todo 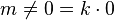 para todo
para todo 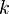 entero.
entero.