Propiedades
 (Propiedad Reflexiva).
(Propiedad Reflexiva).- Si
 y
y  , entonces
, entonces  (Propiedad Transitiva).
(Propiedad Transitiva). - Si
 y
y 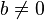 , entonces
, entonces 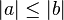 .
. - Si
 y
y  , entonces
, entonces 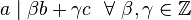 .
. - Si
 y
y , entonces

- Si
 y
y  , entonces
, entonces  .
. - Si
 y
y  , entonces
, entonces  .
. - Para
 ,
,  si y sólo si
si y sólo si 
- Si
 y
y  , entonces
, entonces  .
. - Si
 y
y  cumple que
cumple que  y
y  , entonces
, entonces  .
.  y
y  para todo
para todo  entero ya que
entero ya que 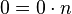 y
y  .
.
Si  no es divisible por
no es divisible por  escribimos
escribimos 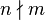 . Notemos que
. Notemos que  para todo
para todo  distinto de cero, pues
distinto de cero, pues 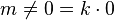 para todo
para todo 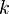 entero.
entero.
 no es divisible por
no es divisible por  escribimos
escribimos 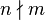 . Notemos que
. Notemos que  para todo
para todo  distinto de cero, pues
distinto de cero, pues 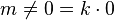 para todo
para todo 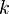 entero.
entero.- El 1 es el único entero que tiene un solo divisor positivo.
- Si d es un divisor de a y no admite más divisor propio que la unidad, se llama divisor primo de a. De hecho es un número primo.
- Si m divide a2, no necesariamente divide a a;2 9 divide 62, pero no divie a 6.
- k primo divide a2 + n2, si solo si k divide a a y divide a n
- La diferencia de cuadrados de dos números de la misma paridad es múltiplo de 4.
- El criterio de divisibilidad está ligado al sistema de numeración y a su base; por ejemplo el número 495 (base 10) en la base 6 se escribe 2143, que será divisible por 5, porque la suma de sus cifras es divisible por 53
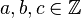 , es decir
, es decir  ,
,  y
y
No hay comentarios:
Publicar un comentario