supongo que A no tiene ningun elemento menor que todos los demas de A
construyamos un B con toda N b+B<a aEa
como ningun elemento es menor que si mismo b esta contenido a
1,2,3,...........b,b+b
b
El principio del buen orden es un lema que establece que todo conjunto que esté formado únicamente por números naturales tiene un primer elemento. Es decir, que el conjunto de los números naturales es bien ordenado. El primer elemento de los números naturales es  .
.
 .
.Demostración del principio del buen orden
Sea  un conjunto no vacío. Si
un conjunto no vacío. Si  no tiene elemento mínimo, entonces existe un conjunto
no tiene elemento mínimo, entonces existe un conjunto  .
.
 un conjunto no vacío. Si
un conjunto no vacío. Si  no tiene elemento mínimo, entonces existe un conjunto
no tiene elemento mínimo, entonces existe un conjunto  .
. debe de estar en
debe de estar en  puesto que de no ser así,
puesto que de no ser así,  sería el elemento mínimo de
sería el elemento mínimo de  .
.- Si cada natural menor o igual a
 está en
está en  , entonces
, entonces  también está en
también está en  , porque de lo contrario,
, porque de lo contrario,  sería un elemento mínimo de
sería un elemento mínimo de 
Luego entonces por el principio de inducción matemática, y
y 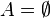 , pero eso contradice la suposición de que
, pero eso contradice la suposición de que  no era un conjunto vacío.
no era un conjunto vacío.
 y
y 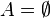 , pero eso contradice la suposición de que
, pero eso contradice la suposición de que  no era un conjunto vacío.
no era un conjunto vacío.
Por lo tanto,  debe tener elemento mínimo.
debe tener elemento mínimo.
 debe tener elemento mínimo.
debe tener elemento mínimo.
No hay comentarios:
Publicar un comentario